A Guide to the Bennett Mechanical Comprehension Test: Examples & Tips
Updated November 18, 2023

- What Is the Bennett Mechanical Aptitude Test?
- What Is the Format of the Bennett Mechanical Comprehension Test?
- Bennett Mechanical Aptitude Test – Example Questions and Answers
empty
empty
empty
- How Is the Bennett Mechanical Comprehension Test Scored?
- How to Prepare for the Bennett Mechanical Aptitude Test
- How to Do Well in the BMCT
- Frequently Asked Questions
- Final Thoughts

The Bennett Mechanical Comprehension Test (BMCT), also referred to as the Bennett Mechanical Aptitude Test, is considered the most popular mechanical aptitude test.
However, it is also believed to be the hardest one to pass.
The BMCT requires you to have a knowledge and understanding of physical principles and answer 55 questions about the application of these concepts within 25 minutes.
You typically need to score in the top 20% of candidates to progress to the next stage of recruitment.
All the questions on the Bennett mechanical comprehension test are multiple-choice and feature an image or a diagram.
As this test can be challenging, this article will help you prepare by:
- Discussing the format of the BMCT
- Working through example questions
- Sharing best practices to help you prepare and pass your Bennett test
What Is the Bennett Mechanical Aptitude Test?
The Bennett Mechanical Comprehension Test was created by Pearson Assessments in the 1940s and is regularly updated.
It is used by companies such as Delta, Coca-Cola and Nestlé as part of the recruitment process for roles such as:
- Firefighters and other emergency services
- Airline engineers and mechanics
- Gas and electrical engineers
- Vehicle mechanics
- Machinery repair engineers
- Plumbers
- Carpenters
- Other engineers
The test is often used alongside other pre-employment tests, such as personality tests, to assess a candidate’s suitability for a job role.
This mechanical comprehension test assesses:
- Mechanical comprehension
- Spatial visualization
- Deduction of how concepts work
- Knowledge of basic physical principles
What Is the Format of the Bennett Mechanical Comprehension Test?
There are two versions of the Bennett Mechanical Comprehension Test.
- The BMCT-I is the pen-and-paper version that has mostly been discontinued, except for in certain circumstances.
- The BMCT-II is the more widely used online version that this article focuses on.
The BMCT-II consists of 55 multiple-choice questions and has a 25-minute time limit.
The online Bennett aptitude test is taken remotely in a location of your choosing and is therefore unsupervised.
However, in certain cases, you might be invited to attend an assessment centre. These locations are often supervised.
Before the test starts, you have the option to complete two practice questions to help familiarize yourself with the computer system, question format and language.
The practice questions are untimed so take as long as you need (within reason) to familiarize yourself.
The questions are in random order and fall into one of the following 12 topics:
- Pulleys and levers – Seven questions on torque and balance
- Hydraulics – Six questions on how liquid moves through a body of water and pipes, buoyant forces and fluid pressure
- Forces, centrifugal force and inertia – Six questions on the effects of a rotating or accelerating object
- Inclined planes – Six questions on kinetic energy, the force needed to push or pull, objects that slide or roll
- Gears and belt drives – Five questions on different types of belt drives, torque and tension; direction, speed and torque of rotating gears
- Gravity and speed – Four questions on how gravity affects an object
- Acoustics and optics – Three questions on sound waves passing through air, liquid and gas; understanding wave refraction and reflection
- Center of gravity – Three questions on where the mass is centered and if an object will fall over
- Electricity – Three questions on circuit diagrams, symbols for various circuit parts, electric charge and resistance
- Heat – Three questions on heat sources and transfer; reading thermometers and pressure gauges
- Forms and volumes – Three questions on formulas to measure volume in various shapes
- Miscellaneous – Six random questions from the topics already covered
Questions are selected from a bank of over 350 so no two Bennett tests are ever the same.
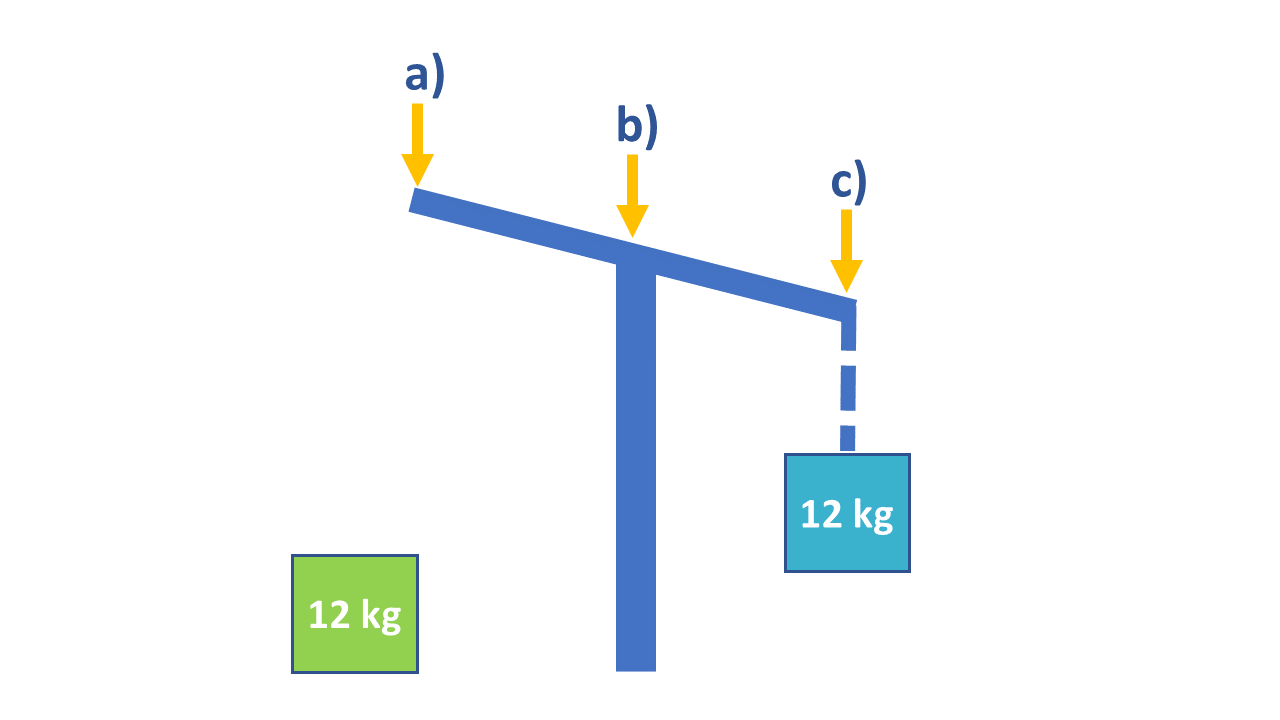
Where would you hang the green box to make the lever balanced?
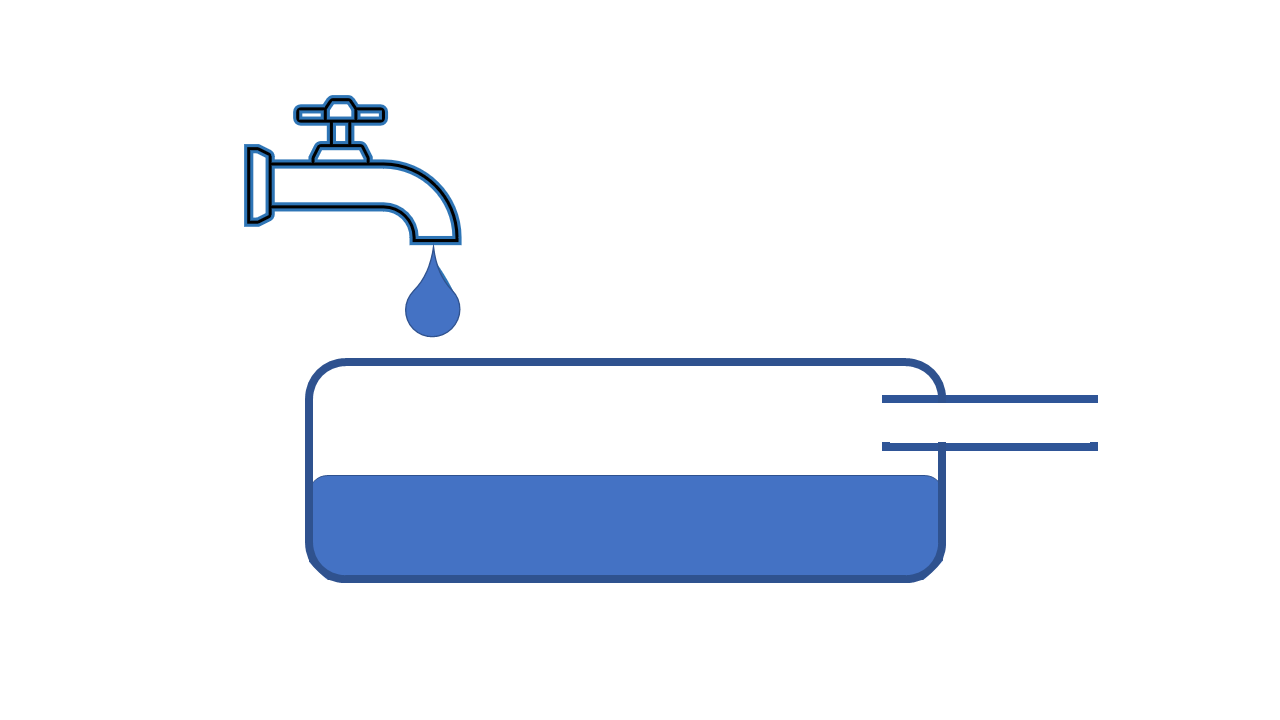
Which direction does the water level move when more water is added?
a) Up
b) Down
c) Stays the same

These two gears are moving together. One has 40 teeth and the other has 60.
How many rotations would the smaller gear have made if the bigger one has made 11?
a) 12
b) 8
c) 16.5
d) 15
How Is the Bennett Mechanical Comprehension Test Scored?
Your Bennett Mechanical Comprehension Test score card will give a:
- Raw score – Number of correct Bennett Mechanical Comprehension Test answers out of 55
- Percentile – The percent of candidates who scored the same or below you
- T-Score – From 10 to 100, standardized and based on how others in your norm performed according to raw scores
- Stanine – From 1 to 9 and used by some companies as an alternative to the T-Score
- Sten – From 1 to 10 and used by some companies as an alternative to the T-Score and stanine score
There are eight occupational norms and two industry norms.
The occupational norms are:
- Installation/maintenance/repair
- Skilled trades
- Machine operators/machinists
- General labor
- Vocational/technical students
- Mechanics
- Engineers
- Industrial/technical sales
The industry norms are:
- Energy and utilities
- Manufacturing and production
These roles are highly competitive, and the employer decides on the passing score. You want to aim for 80% or above to have a chance of being invited to the next stage of recruitment; this equates to a raw score of at least 44.
As these tests are part of the recruitment process, it is unlikely that you will have the opportunity to retake them should you fail. Your recruitment officer will advise you on the best steps to take if this happens.
How to Prepare for the Bennett Mechanical Aptitude Test
To pass the Bennett Mechanical Comprehension Test you will need to properly prepare.
The best way to do this is to:
Step 1. Practice the Test Format and Question Types
There are several great online resources such as WikiJob and JobTestPrep that offer Bennett mechanical comprehension practice tests, while others offer materials like Bennett Mechanical Comprehension Test answer keys.
Some come with a fee, but there are many free mechanical comprehension tests available.
If you think you would benefit from a paid package and you have the budget, make the investment. The paid resources typically have multiple tests and are more similar to the real thing.
Otherwise, working through the free practice tests and Bennett aptitude test study guides will help familiarize you with the language and format of the questions.
Step 2. Practice Timing and Working Under Pressure
When you first start preparing, work through the questions at your own pace. As you become more confident, begin adding time limits.
If it took you 60 minutes to finish your last practice test, work to a time limit of 55 minutes next time. Reduce this by five minutes on each attempt until you are comfortable with the 25-minute limit.
Step 3. Go Over Basic Concepts Related to the Test
The basic concepts needed for the Bennett Mechanical Comprehension Test are:
- Newton’s three laws of motion, friction and gravity
- The ideal gas law
- Bernoulli’s principle
- Ohm’s law
- The Doppler effect
- Principles of light, reflection and sight
- Evaporation and condensation
- Circuits
- Rotational and linear velocity
- Attenuation
Step 4. Practice the Principles
As well as having a basic understanding of these principles, physically seeing them in action will help you work through the questions more quickly.
- Newton’s three laws of motion, friction and gravity – This includes equal and opposite reactions, such as a magnet attracting a paperclip or a horse pulling a carriage
- The ideal gas law – How vehicle airbags inflate or why a basketball shrinks in the cold
- Bernoulli’s principle – How an aircraft takes off, why a spinning ball curves in the air or how chimneys work
There are everyday examples of how these mechanical principles work that can make them less scientific or complicated.
If it is safe to do so, test them out and see them in action.
Having this visual representation will help you visualize what a question is asking.
Step 5. Give Yourself Enough Time to Prepare
Set aside time every day to work through your study regime. Leaving your practice to the last minute will only cause you more stress.
Step 6. Gather as Much Information as Possible
- Read through several websites that offer Bennett aptitude test study guides and advice
- Consult the official test site
- Ask questions on Reddit or Quora
- Clarify anything you don’t understand with your recruitment officer
The more information you gather, the fewer surprises you’ll have on the day.
How to Do Well in the BMCT
On the day of the test:
- Ensure you have prepared everything you need beforehand
- Read each question carefully
- Be aware of the time
- Don’t linger on one question for too long; move on if you are stuck
- Use the elimination technique by disregarding the definite incorrect answers and making an educated guess from the options remaining
Frequently Asked Questions
The Bennett Mechanical Comprehension Test is a pre-employment aptitude test designed to measure your understanding of physical principles relevant to specific job roles.
It consists of 55 multiple-choice questions and has a 25-minute time limit.
The Bennett Mechanical Comprehension Test is difficult if you haven’t taken enough time to prepare.
Those with an understanding of the principles and concepts assessed will have little difficulty completing the questions.
Several websites can help you prepare for your Bennett Mechanical Comprehension Test.
WikiJob, Psychometric-Success and JobTestPrep all have definitive guides and practice tests for you to work through.
The topics included in the Bennett Mechanical Comprehension Test are pulleys and levers, hydraulics, forces, centrifugal force and inertia, inclined planes, gears and belts, gravity, acoustics and optics, electricity, heat and volume.
After you have completed the Bennett Mechanical Comprehension Test, you will receive a call or email from your recruitment officer informing you if you have made it to the next stage of the application process.
To ace the Bennett Mechanical Comprehension Test, you will need to properly prepare by working through practice tests, answering under timed conditions and learning basic principles such as Ohm’s law and Newton’s three laws.
There are 55 multiple-choice questions and a 25-minute time limit.
Free Bennett Mechanical Comprehension Tests are available online at WikiJob, Psychometric-Success and JobTestPrep.
The jobs that require passing the Bennett Mechanical Comprehension Test are firefighters, airline engineers and mechanics, engineers, vehicle mechanics, machinery repair technicians, plumbers and carpenters.
65% would not be considered a good score for the Bennett Mechanical Comprehension Test. Most employers only accept 80% or higher.
However, if a majority of the candidates were to perform below 65%, your employer may consider it a good score.
The Bennett test is a pre-employment test and therefore cannot be retaken in the same application period.
However, your recruiter may make exceptions in extenuating circumstances.
You can find more helpful tips on taking the Bennett Mechanical Comprehension Test at WikiJob, JobTestPrep, Reddit and Quora.
Final Thoughts
The Bennett Mechanical Comprehension Test is a pre-employment test designed to highlight candidates with the necessary knowledge for a specific job role.
While the test is designed to be challenging, with enough preparation it is possible to score in the top percentile.
Before taking the test:
- Complete as many practice questions as possible
- Learn and understand all the essential principles and concepts
- Familiarize yourself with the test and question formats
- Have confidence in your skills and ability